Como Explicar Fracciones A Niños De Cuarto Grado: Un Enfoque Didáctico es un tema crucial en la educación matemática. Las fracciones, a menudo consideradas abstractas, son en realidad conceptos fundamentales que se encuentran presentes en la vida cotidiana. Desde dividir una pizza con amigos hasta medir ingredientes en una receta, las fracciones nos ayudan a comprender y manipular cantidades de manera precisa.
Este artículo explora estrategias para introducir las fracciones a los niños de cuarto grado de forma clara, atractiva y práctica, haciendo que el aprendizaje sea significativo y memorable.
La comprensión de las fracciones es esencial para el desarrollo del pensamiento matemático. Proporciona una base sólida para conceptos más avanzados como las proporciones, los porcentajes y las ecuaciones. Enseñar fracciones a los niños de cuarto grado requiere un enfoque didáctico que combine la teoría con la práctica, utilizando ejemplos del mundo real y actividades interactivas que les permitan visualizar y experimentar estos conceptos.
Introducción
Las fracciones son una parte fundamental de las matemáticas y se encuentran presentes en muchas situaciones de la vida cotidiana. Desde dividir una pizza con amigos hasta medir ingredientes para una receta, las fracciones nos ayudan a comprender y representar cantidades que no son enteras.
En este artículo, exploraremos el fascinante mundo de las fracciones, aprendiendo cómo funcionan y cómo se pueden aplicar en diferentes contextos.
Las fracciones son como pedazos de un todo. Imagina una deliciosa pizza cortada en 8 rebanadas iguales. Cada rebanada representa una fracción de la pizza completa. Si te comes 3 rebanadas, estás comiendo 3/8 de la pizza. El número de abajo (8) nos dice en cuántas partes se dividió la pizza, mientras que el número de arriba (3) nos dice cuántas partes estamos tomando.
Ejemplos de Fracciones en la Vida Cotidiana
- Tiempo:Si un programa de televisión dura una hora (60 minutos) y ya han pasado 20 minutos, entonces ha transcurrido 20/60 de la hora total, que se puede simplificar a 1/3 de la hora.
- Ingredientes:Una receta puede pedir 1/2 taza de azúcar o 3/4 de taza de harina. Estas fracciones indican las cantidades precisas de cada ingrediente.
- Distancias:Si viajas en un tren y el recorrido total es de 100 kilómetros, y ya has recorrido 30 kilómetros, has completado 30/100 del viaje total, que se puede simplificar a 3/10 del viaje.
Conceptos Básicos de Fracciones
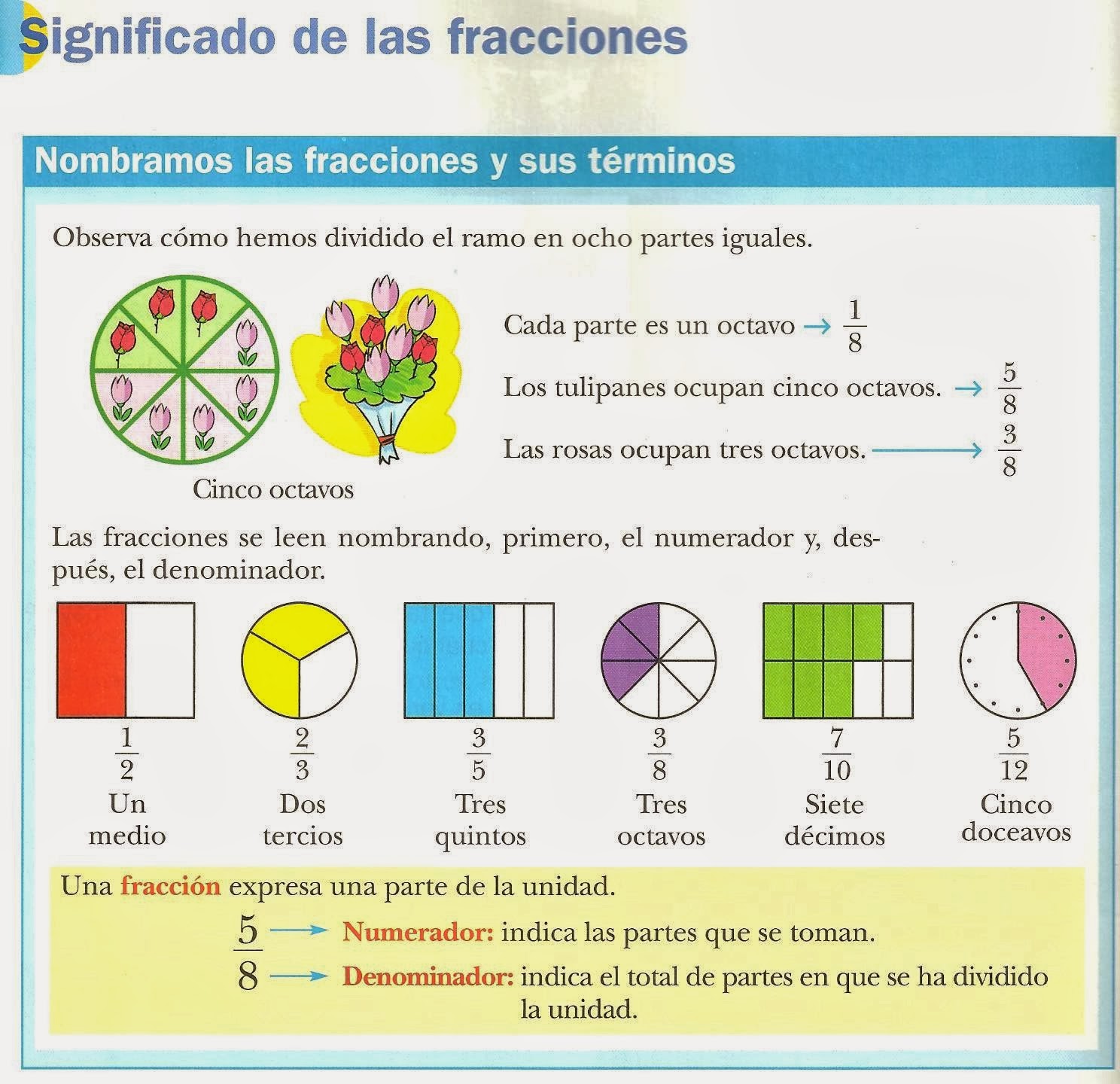
Una fracción representa una parte de un entero. Está compuesta por dos números: el numerador y el denominador.
Numerador y Denominador
El numeradorindica cuántas partes del entero estamos tomando. Se escribe en la parte superior de la fracción.
El denominadorindica en cuántas partes iguales se ha dividido el entero. Se escribe en la parte inferior de la fracción.
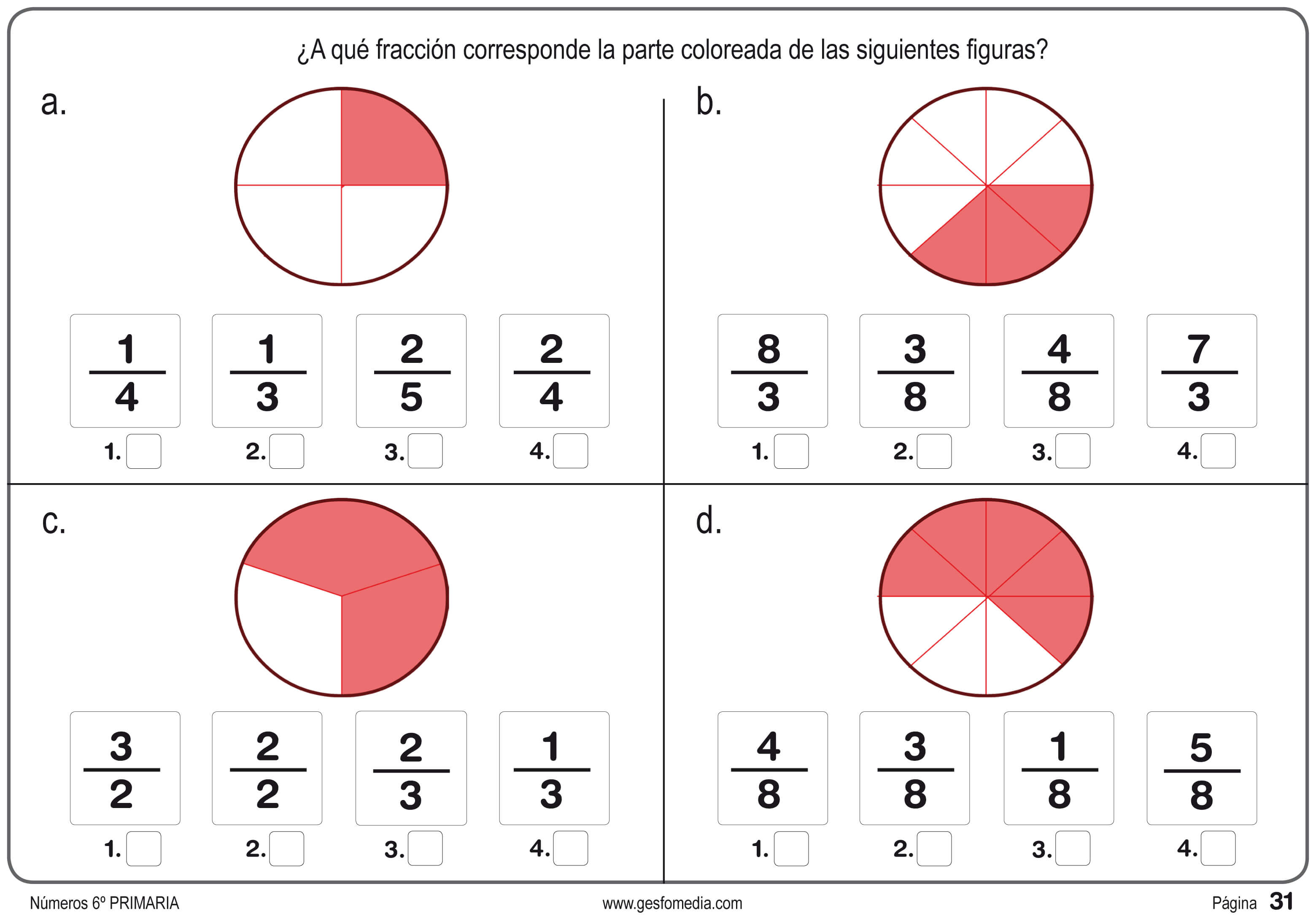
Representación Gráfica de Fracciones
Las fracciones se pueden representar gráficamente utilizando círculos o barras divididas en partes iguales. Por ejemplo, la fracción 2/5 se puede representar como un círculo dividido en 5 partes iguales, donde 2 de esas partes están sombreadas.
Relación entre el Numerador, el Denominador y el Tamaño de la Fracción
El tamaño de una fracción depende de la relación entre el numerador y el denominador. Si el numerador es más pequeño que el denominador, la fracción es menor que 1. Si el numerador es igual al denominador, la fracción es igual a 1.
Si el numerador es mayor que el denominador, la fracción es mayor que 1.
Tipos de Fracciones
Existen diferentes tipos de fracciones, cada una con sus propias características:
Fracciones Propias
Las fracciones propias tienen un numerador menor que el denominador. Por ejemplo, 1/2, 3/4 y 5/8 son fracciones propias.
Fracciones Impropias
Las fracciones impropias tienen un numerador mayor o igual que el denominador. Por ejemplo, 5/4, 7/3 y 9/2 son fracciones impropias.
Fracciones Mixtas
Las fracciones mixtas combinan un número entero con una fracción propia. Por ejemplo, 1 1/2, 2 3/4 y 3 1/3 son fracciones mixtas.
Equivalencias de Fracciones: Como Explicar Fracciones A Niños De Cuarto Grado
Las fracciones equivalentes representan la misma cantidad, aunque se escriban de forma diferente. Para encontrar fracciones equivalentes, se multiplica o divide el numerador y el denominador de la fracción original por el mismo número.
Ejemplo de Fracciones Equivalentes
| Fracción | Representación Gráfica |
|---|---|
| 1/2 | [Imagen de un círculo dividido en 2 partes iguales, con una parte sombreada] |
| 2/4 | [Imagen de un círculo dividido en 4 partes iguales, con 2 partes sombreadas] |
| 3/6 | [Imagen de un círculo dividido en 6 partes iguales, con 3 partes sombreadas] |
Suma y Resta de Fracciones
Para sumar o restar fracciones con el mismo denominador, se suman o restan los numeradores y se mantiene el mismo denominador.
Ejemplo de Suma de Fracciones
1/4 + 2/4 = (1 + 2)/4 = 3/4
Ejemplo de Resta de Fracciones
3/5 – 1/5 = (3 – 1)/5 = 2/5
Multiplicación de Fracciones
Para multiplicar fracciones, se multiplican los numeradores y los denominadores.
Ejemplo de Multiplicación de Fracciones, Como Explicar Fracciones A Niños De Cuarto Grado
1/2 – 3/4 = (1 – 3) / (2 – 4) = 3/8
División de Fracciones
Para dividir fracciones, se invierte la segunda fracción y se multiplican las dos fracciones resultantes.
Ejemplo de División de Fracciones
1/2 / 3/4 = 1/2 – 4/3 = (1 – 4) / (2 – 3) = 4/6
Aplicaciones de las Fracciones
Las fracciones se utilizan en muchos ámbitos de la vida real, como:
- Cocina:Las recetas suelen indicar las cantidades de los ingredientes en fracciones.
- Construcción:Los planos de construcción utilizan fracciones para indicar las dimensiones de las estructuras.
- Finanzas:Los intereses de los préstamos y las inversiones se expresan en fracciones.
Top FAQs
¿Cuáles son los recursos más efectivos para enseñar fracciones a los niños de cuarto grado?
Los recursos más efectivos incluyen materiales manipulativos como bloques de fracciones, pizzas de papel, barras de chocolate, juegos de mesa y aplicaciones educativas que permiten a los niños visualizar y experimentar las fracciones de forma práctica.
¿Cómo puedo motivar a los niños a aprender sobre fracciones?
La motivación se logra al conectar las fracciones con la vida real, utilizando ejemplos interesantes y actividades divertidas. También es importante crear un ambiente de aprendizaje positivo y colaborativo donde los niños se sientan libres de explorar y experimentar.
¿Qué estrategias puedo usar para evaluar la comprensión de las fracciones en los niños?
Las estrategias de evaluación incluyen la observación de la participación en actividades prácticas, la resolución de problemas de fracciones, la realización de pruebas escritas y la creación de proyectos que demuestren su comprensión.
